Write-up for HCMUS-CTF Warm-Up Stage - CRYPTOGRAPHY

SanityCheck

MQZGQ3K2PFBDMYTONB4USR3YNFQUGQTJLEZUU2CJI5UGUSKHPBUWCR2VM5RW26DZLJTW6S2WKZBGCU2FLF2FKRLEKRSTA4DZLAZDK3DDNQ4VAZKXGV3WKR2OGJMVQ2DZLJLDS4LDNZWHOWLOOB4VQMTENFMDGVTXMVWWQ3KYGNBG4YZRHB4U2RCJPBTFCPJ5  

Guess that the message is encoded in Base32

base64.b32decode(s32).decode()

d2hmZyB6bnhyIGxiaCBiY3JhIGhjIGxiaGUgcmxyZgoKVVBaSEYtUEdTe0pyX25lcl9PeW5weGN2YXhyZV9qcnlwYnpyX2diX3VwemhmX3Bnc18yMDIxfQ==

You see == at the end => It’s Base64 encode

base64.b64decode(s64).decode()

whfg znxr lbh bcra hc lbhe rlrf

UPZHF-PGS{Jr_ner_Oynpxcvaxre_jrypbzr_gb_upzhf_pgs_2021}

UPZHF-PGS{Jr_ner_Oynpxcvaxre_jrypbzr_gb_upzhf_pgs_2021} is similar to the flag format and UPZHF-PGS ~ HCMUS-CTF => Caesar Cipher - shift by key = 13

==> Flag: HCMUS-CTF{We_are_Blackpinker_welcome_to_hcmus_ctf_2021}

SingleByte

r4SJmJOanoOFhMqDmcqLyp2Lk8qFjMqZiZiLh4iGg4SNyo6LnovKmYXKnoKLnsqFhIaTyoufnoKFmIOQj47KmouYnoOPmcqJi4TKn4SOj5iZnouEjsqego/Kg4SMhZiHi56DhYTEyqOEyp6PiYKEg4mLhsqej5iHmcbKg57Kg5nKnoKPypqYhYmPmZnKhYzKiYWEnI+YnoOEjcqCn4eLhMeYj4uOi4iGj8qahouDhJ6Pkp7KnoXKg4SJhYeamI+Cj4SZg4iGj8qej5KexsqLhpmFyoGEhZ2EyouZyomDmoKPmJ6Pkp6iqae/ucepvqyRnY+1gYSFnbWegouetZOFn7WJi4S1joW1mYOHmoaPtbKluLXf3tnb2dvf3ouIiYyP396LjNiPiYuIlw==

== at the end => Base64 encode

s = base64.b64decode(s64).decode()

The title is single byte encode. Do u find it familiar ?? => XOR encode
Also, remember format of the flag: HCMUS-CTF{…}. The key may be

k = s[0] ^ ord('H')

or

k = s[1] ^ ord('C')

=> Try all possible key and finally i succeed.

k = s[-1] ^ ord('}')
print(''.join(chr(c ^ k) for c in s))

Encryption is a way of scrambling data so that only authorized parties can understand the information. In technical terms, it is the process of converting human-readable plaintext to incomprehensible text, also known as ciphertextHCMUS-CTF{we_know_that_you_can_do_simple_XOR_54313154abcfe54af2ecab}

==> Flag: HCMUS-CTF{we_know_that_you_can_do_simple_XOR_54313154abcfe54af2ecab}

TheChosenOne

Given an AES-ECB encryption oracle. The problem is a basic AES-ECB blockcipher Chosen Plaintext Attack.
First, you should determine the size of the block. Look into the given script server.py

def padding(plaintext):

    plaintext_length = len(plaintext)
    padding_length = 0
    
    if plaintext_length % 32 != 0:
        padding_length = (plaintext_length // 32 + 1) * 32
    else:
        padding_length = 0
    return padding_length

Guess that the blocksize is 32. However, you can verify by sending from 1 to n characters to find the block size. Second, you should find the offset if chosen plaintext does not start as the first byte of a block. But in this challenges, it’s easier than expected. The server code shows that our plaintext appear as first part of text for encryption.

def main():
    flag = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # TODO 
    key = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # TODO
    
    padding_character = "D"
    
    assert (len(flag) == 32) and (len(key) == 32)
    cipher = AES.new(key, AES.MODE_ECB)

    banner = """

    inp = ''
    if rlist:
        user_input = sys.stdin.readline().rstrip('\n')

    plaintext = user_input + flag
    padding_length = padding(plaintext)
    plaintext = plaintext.ljust(padding_length, padding_character)
    
    sys.stdout.write('The ciphertext:\n{}\n\n'.format((cipher.encrypt(plaintext)).encode('hex')))

Another useful information is the length of flag = 32.
Attack!
Idea of the attacking method is sending blocksize - 1 byte for the encryption oracle and the last byte of block is the first of the flag. Then you just bruteforce to find that character. Repeating doing this for the rest of the flag.

index = 0
res = []
while True:
    inp_str = 'A' * (31 - index)
    sendline(inp_str)

    cipher_text = recv_cipher()
    try_inp_str = inp_str

    for j in res:
        try_inp_str += j
    for i in range(32, 126):
        tmp_inp_str = try_inp_str + chr(i)
        sendline(tmp_inp_str)

        try_cipher_text = recv_cipher()
        if try_cipher_text[:64] == cipher_text[:64]:
            res.append(chr(i))
            break
    index += 1
    if index > 31:
        break
print(''.join(res))

==> Flag: HCMUS-CTF{You_Can_4ttack_A3S!?!}

Crackme

$6$OQy2HYdK1F0RuFLv$OEsWe98lUzVkAiZy0.BDj.1GwjRtD72QZtQ7XugSdGss6TEXxnu4b3NWaVKBoSFtJ/LlG59l2sh4nLUPIqeLV1

Crack that hashed to plaintext. The base64 of the plaintext is the password to open the zip file.

The format of the hash is $6$rounds={rounds}${salt}${checksum} and it’s SHA512
==> Use hashcat tool with rockyou wordlist to crack that file

base64.b64decode(b'playboy123').decode()

b'cGxheWJveTEyMw=='

=> Password to unzip phase2.zip: cGxheWJveTEyMw==

In the phase2, you should crack id_rsa file to unzip flag.zip containing flag

Crack it to find the passphrase. The password to opened the zip file is the base64 of that passphrase.

==> Use John the Ripper to crack that file with wordlist rockyou!

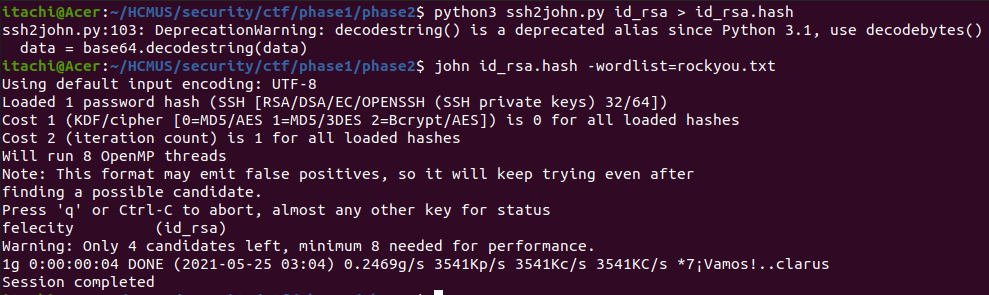
==> Get the key: felecity 

base64.b64decode(b'felecity').decode()

b'ZmVsZWNpdHk='

=> Password to unzip flag.zip: ZmVsZWNpdHk=

==> Flag: HCMUS_CTF{cracking_for_fun}

RSB

Focus on RSA Decryption using Chinese Remainder Theorem. You will get some insights from author’s code.

def crt(a: List[int], m: List[int]) -> int:

    M = 1
    for mi in m:
        M *= mi

    x = 0
    for i in range(len(a)):
        a_i = a[i]
        m_i = m[i]

        M_i = M // m_i
        y_i = pow(M_i, -1, m_i)

        x = (x + a_i * M_i * y_i) % M
    return x

def decrypt(c: int) -> int:
    """
    What's happening here?
    I compute:
        m_p = c^d mod p
        m_q = c^d mod q

    Then apply CRT to compute m

    Why?
    I heard that this approach is 4 times faster than the usual c^d mod N
    """

    # Compute c^d mod p
    m_p = 1
    a = c
    k = d
    while k > 0:
        if k % 2 == 1:
            m_p = m_p * a % p
        a = a * a % p
        k = k // 2

    # Compute c^d mod q
    m_q = 1
    a = c
    k = d
    while k > 0:
        if k % 2 == 1:
            m_q = m_p * a % q
        a = a * a % q
        k = k // 2

    return crt([m_p, m_q], [p, q])

Dive into the decrypt function, there’s an abnomal line.

while k > 0:
    if k % 2 == 1:
        m_q = m_p * a % q
    a = a * a % q
    k = k // 2

So, output of this function become

\(m_p = c^d mod(p)\)
\(m_q = m_p * c^k mod(q)\) with \(k=c^{\left\lfloor{\log_c^d}\right\rfloor}\)

So when choosing \(c_2 = c_1^2\):
\(k_2 = c_2^{\left\lfloor{\log_{c_2}^d}\right\rfloor}=c_1^{2\left\lfloor{\log_{c_1^2}^d}\right\rfloor} = c_1^{\left\lfloor{\log_{c_1}^d}\right\rfloor} = k1\)

After feeding to crt(), we get:
\(x = (a_0 * M_0 * y_0 + a_1 * M_1 * y_1) mod(M)\) \(= (m_p * q * q^{-1} mod(p) + m_q * p * p^{-1}mod(q)) mod(pq)\) \(= (c^d mod(p))(qq^{-1}mod(p) + c^kmod(q)pp^{-1}mod(q))mod(pq)\)

Then try to decrypt with \(c_1=2, c_2=c_1^2=4\). We get \(x_1\), \(x_2\) and based on above results:
\(x_1^2-x_2 = 0 mod(p)\)
\(p = gcd(x_1^2-x_2, N)\)
After this step, the following operators are quite simple

q = N // p
phi = (q-1)*(p-1)
d = inverse(e, phi)
flag = long_to_bytes(pow(c, d, N))

==> Flag: HCMUS-CTF{fault-attack}